Contenido del Articulo
Plan de lecciones:
Modelos matemáticos
Nombramiento de los modelos matemáticos
Clasificación de los modelos matemáticos
Listas, tipos, propósito, características
Formas de crear listas en Word
Modelos matemáticos
Leamos un misterio tan simple:
“Mamá sirvió a tres niños un jarrón entero de sus chocolates favoritos. Los niños no podían esperar a que los dulces fueran compartidos, así que empezaron a comerlos lentamente. Anton de 5 años tomó 6 pedazos y se los comió, Irina de 10 años tomó la mitad de lo que quedaba. Y Igor, de 3 años, recibió un tercio de todos los caramelos que su madre compró. Cuando llegó mamá, los niños discutían que los caramelos no se compartían honestamente. Pero ella los calmó, que todos eran iguales.
Hay mucha información en este pasaje: los dulces favoritos, cuántos hijos tuvo mamá, sus nombres y edad, así como quiénes, cuánta azúcar comieron. Pero para saber si los niños se dividieron el trato honestamente, sólo necesitas algunos datos.
La construcción de un modelo matemático de esta historia:

Fuente.
Registra el modelo matemático: x-6-1/2*(x-6)=1/3*x.
Resulta que el primer niño tomó 6 dulces, el segundo – (18-6)/2=6, el tercero – 18/3=6. Entonces, mamá tenía razón, todos los niños comieron la misma cantidad de dulces.
Así que la solución del modelo matemático permitió a la madre reconciliar a los niños.
Los modelos matemáticos son descripciones cuantitativas de las relaciones entre objetos o procesos.
En otras palabras, un modelo matemático es una expresión de un proceso u objeto utilizando fórmulas, signos y números. Naidya, marca la regla con un campo rojo, por favor.
Lo que acabamos de hacer se llama modelado matemático, es decir, reemplazar la información original de una manera matemática. Este es el enfoque más lógico para describir algo más tarde con un programa de ordenador.
Es más fácil investigar un modelo matemático escribiendo un algoritmo computacional que permite calcular y resolver cualquier tarea de este tipo.
Nombramiento de los modelos matemáticos
Ámbito de aplicación del modelado:

Fuente.
El modelado matemático es muy utilizado: modelos económicos y matemáticos, previsiones financieras, cálculos de ingeniería. Permite estudiar, analizar y predecir.

Fuente.
Significa que un experimento real puede realizarse varias veces, se puede escribir un modelo matemático del proceso y luego, utilizando un programa de computadora o cálculos manuales, “ejecutar” los otros valores sin experimentar.
Por ejemplo, para alimentar el pastel a 1 persona, calcula cuántos trozos necesita hasta la saturación. Calcule el tamaño del pastel si los invitados son 10, 20, 100 personas.
Utiliza el lenguaje matemático: fórmulas, signos, símbolos, números, ecuaciones, sistemas de ecuaciones. Este es uno de los métodos más utilizados y exactos de investigación científica.
Cálculos de las reacciones nucleares, la cantidad de calor liberado, la radiación – todo esto es mejor calcularlo teóricamente, pero verificarlo experimentalmente sólo parcialmente. El estudio de las infinitudes cósmicas, las profundidades oceánicas, todavía es posible sólo matemáticamente, pero cuanto más se domina el cielo y el océano, más a menudo se está convencido de la corrección de los cálculos.
La química, la física y la economía son difíciles de imaginar sin modelos matemáticos. Ahora los biólogos, ecologistas y médicos también han comenzado a utilizar ampliamente la programación matemática. Por ejemplo, los científicos de todo el mundo están calculando ahora periódicamente el número de personas que se verán afectadas por la pandemia. Además, actualizan constantemente sus previsiones introduciendo nuevos datos sobre la mortalidad y la recuperación, sobre la persistencia del virus en diferentes condiciones.
Un ejemplo:
Para mantener a las gallinas ponedoras, hay que saber cuánto y qué alimento se necesita para mantener a una gallina por día. Si compras sin pensar forraje mezclado, grano, verdura, el pájaro seguirá hambriento, porque parte de la materia prima se echará a perder, los insectos, y algo no es suficiente. Es más lógico calcular de antemano cuánto y qué comprar (+ pequeñas existencias) y sólo entonces empezar a poner gallinas.
Sabemos cuánta comida se necesita por día para una gallina ponedora. Unos 300 g por día, teniendo en cuenta la composición (86 g de trigo, 16 cortes, 44 de maíz y cebada, 32 de maquis, avena, guisantes, 10 de tiza, harina de harina de pescado y carne, 6 g de levadura).
¿Y el día para 10, 80, 150, 758 pájaros? ¿Y durante 3 meses?
Los datos de 1 pollo se obtienen experimentalmente, y el cálculo de cualquier otra cantidad se obtiene por medio de cálculos.
Teniendo un modelo, puedes obtener cálculos para cualquier especie de ave y cualquier cantidad, porque el enfoque será similar.
Por lo tanto, este método permite reducir y a veces evitar completamente los experimentos, lo que es muy importante cuando los recursos son limitados, costosos o peligrosos.
Las ventajas del modelado matemático:
- la capacidad de reemplazar los experimentos reales;
- lo barato del proceso;
- la capacidad de cambiar los componentes, los pasos del proceso, pasando por todo tipo de opciones;
- análisis de la influencia de diversos factores y condiciones;
- una forma de estudiar los objetos que son inaccesibles para los humanos (nacimiento de estrellas, agujeros negros).
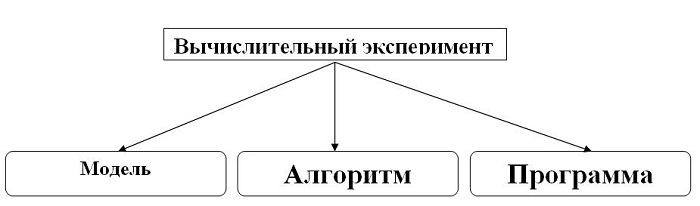
Así que, el modelado matemático es el mismo experimento, sólo que calculado, computacional. Por eso necesitamos un plan de secuencia claro que contenga 3 pasos:
- Compilar un modelo matemático.
- Escribiendo el algoritmo.
- Programación de algoritmos.
Fuente.
En la primera etapa hay una descripción del modelo matemático – los procesos que ocurren, las dependencias entre los objetos se expresan por medio de ecuaciones.
Los modelos pueden capturar todas las conexiones y procesos, pero es necesario elegir sólo los parámetros significativos para construir el actual modelo simplificado. Si se capturan y describen todos los factores, se tendrá que invertir una cantidad irrazonable de tiempo y recursos para construir tal estructura, además de que en los algoritmos complejos hay errores más frecuentes, y encontrarlos no es fácil.
El siguiente paso es construir un algoritmo que cumpla con los criterios básicos:
- Corresponde al modelo original.
- Reconstruido para tales tareas.
- Ahorra tiempo.
- Te da un resultado que te conviene exactamente.
- Adecuado para la programación de ordenadores.
En la tercera etapa, se crea un programa que también corresponde a las características descritas anteriormente.
Clasificación de los modelos matemáticos
Todos los modelos pueden dividirse por tipo, propósito, contenido y otros parámetros. A menudo se encuentran especies mixtas.
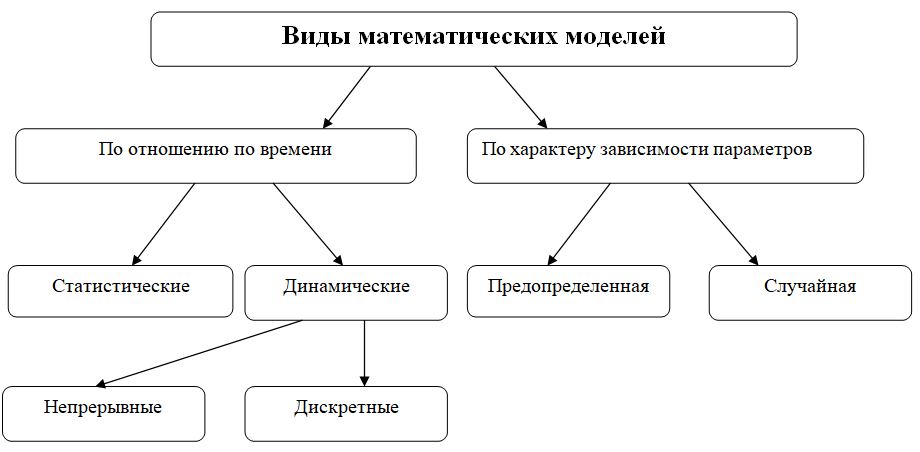
Modelo estadístico en relación con el tiempo: cuántos pasteles y jugos hay que comprar para hacer una mesa de dulces para los escolares.
Dinámica – dinámica de cambio en el precio de los huevos, el petróleo, y cambio en el costo de la torta terminada mensualmente.
Un modelo discreto describe el comportamiento de un objeto en un punto específico en el tiempo, por ejemplo, la energía de un electrón en el átomo de hidrógeno.
El modelo continuo nos permite estudiar el cambio constante en la altitud del nivel del océano a partir de la temperatura del aire en el planeta.
Modelo predeterminado por la naturaleza de la dependencia de los parámetros – cálculo de la calidad del grano con los cambios de temperatura y humedad en el almacén.
Al azar – una descripción del movimiento del cometa. En este caso hay una descripción real de varios parámetros, ya que es imposible influir en ellos.
Es importante desmontar la tarea en cálculos simples, dependiendo del objetivo. En el ejemplo de la gallina, puede necesitar la cantidad de alimento que necesita desde el momento en que la gallina comienza a poner huevos hasta el declive o el cese completo de la producción de huevos. Entonces tienes que contar con toda la cantidad de alimento, pero para diferentes cabezas y para diferentes términos.
Dado que un tercio de la composición diaria es trigo y sus productos, se puede calcular cuánto sembrar (sabiendo que su rendimiento medio es de 4,5 t/ha en primavera o de 5,8 t/ha en invierno) para proporcionar 1000 cabezas de gallinas ponedoras. El grano y el salvado de trigo constituyen casi el 32% de la alimentación. El resto de los componentes deben ser comprados o calculados por analogía.
Listas, tipos, propósito, características
El modelado matemático es imposible sin un algoritmo de acción o un plan de acción paso a paso. Tal lista con números de paso es una lista de muestra. Las listas nos rodean por todas partes.
Mira los diarios, las paredes de la oficina, el libro de texto. Estos son el horario de clases, el tráfico, la receta, la lista de tareas, la lista de cumpleaños y muchos otros ejemplos.

Listas – una forma de presentar información para describir algo o para listar objetos.
En la mayoría de los casos se utilizan tres tipos principales de listas:
- Marcado – al principio de cada punto hay un símbolo especial (marcador). Puede ser un punto, un asterisco y mucho más. La mayoría de las veces se usa para simplemente enumerar algo.
- Numerados – en lugar de marcadores utilizan un número de serie (dígitos romanos o arábigos, letras del alfabeto o incluso un numerador con una palabra). Es conveniente para registrar el orden de las acciones, la lista de componentes, las instrucciones paso a paso, el algoritmo.
- Multi-nivel – una lista con etiquetas. En ella los puntos están dispuestos jerárquicamente, es decir, por niveles. El número total de niveles puede ser de 9. Los marcadores/números de los artículos y subítems pueden ser seleccionados cualquiera.
Para todos los tipos de listas puedes cambiar el tamaño, el color, el trazo tanto de los marcadores/números como de los elementos (para ellos también puedes cambiar la fuente). Por el tipo de bala (marcador) se pueden distinguir diferentes tipos de listas marcadas.
Por lo que se utilizó como marcador (números, letras, caracteres), las listas numeradas se dividen en diferentes tipos.
Una de las formas más fáciles y convenientes de crear listas es escribirlas en un editor de texto. Es muy fácil de hacer y lo puede hacer cualquiera que esté un poco familiarizado con Word.
Formas de crear listas en Word
Para hacer listas en el editor de texto de Word, puede utilizar uno de los métodos sugeridos:
- La primera forma de crear una lista marcada es la más frecuente. Coloque el cursor del ratón en el lugar deseado del documento, seleccione la pestaña del párrafo en el Panel Principal, pase el ratón por encima del menú desplegable de la lista marcada/numerada o de varios niveles.
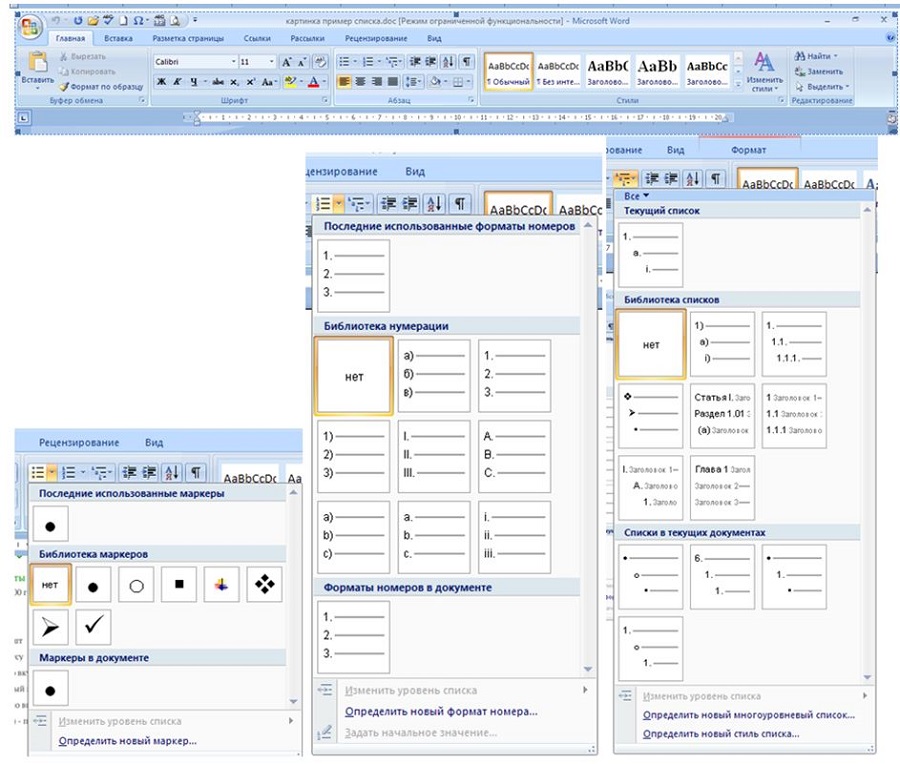
Seleccione el tipo de marcador adecuado. Empieza a escribir el texto. Cada nueva línea (después de Intro) se considera un nuevo elemento, lo que significa que estará con el marcador seleccionado.
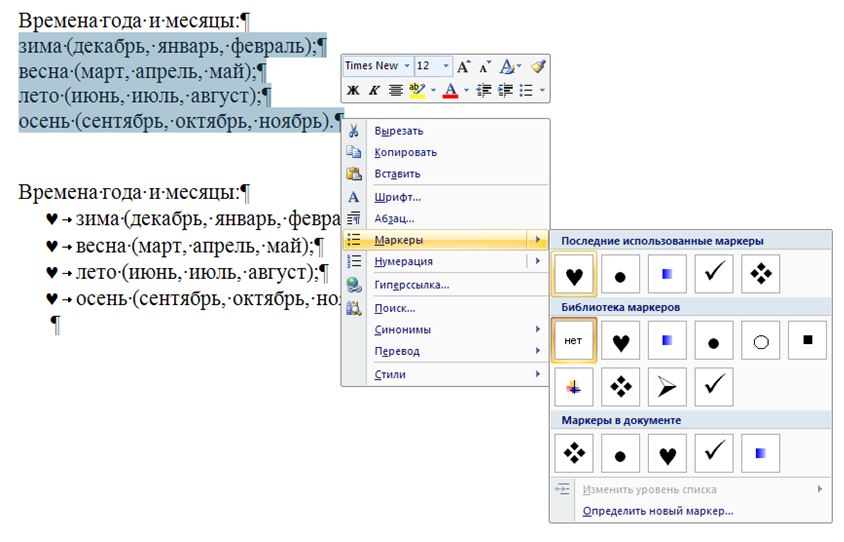
Ejemplo de una lista marcada:
Estaciones y meses:

Una lista numerada se hace de la misma manera:
Estaciones y meses:

¡Importante! Una buena regla de tono es empezar con una letra pequeña y terminar con un punto y coma. La lista numerada comienza con una letra mayúscula y termina con un punto y coma.
Ejemplos, tipos de lista de varios niveles:
Estaciones y meses:

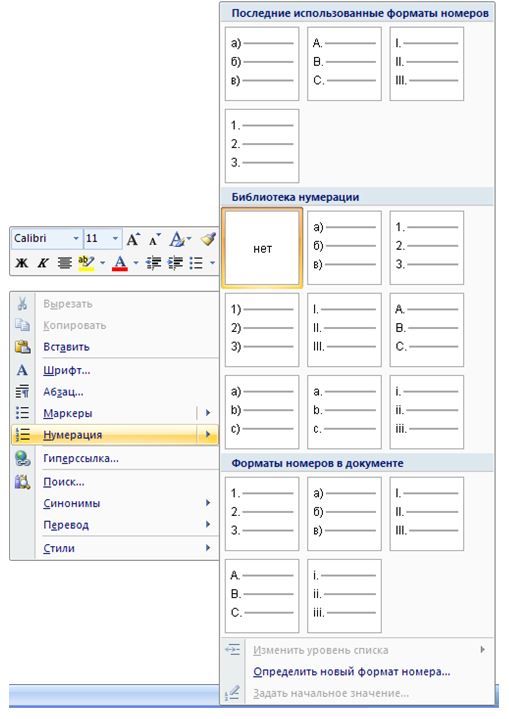
La segunda forma de crear una lista numerada o de otro tipo es utilizar el menú contextual, el botón derecho del ratón (PCM).
Ponga el cursor en el lugar deseado del documento, pulse PCM, seleccione Marcadores o Numeración.
Para la versión del marcador:
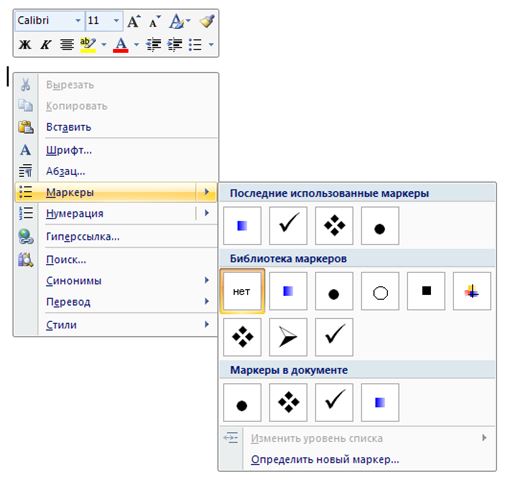
Para la opción de numeración:
Puede convertir la información en una lista. Para ello, seleccione las líneas mecanografiadas y luego seleccione el tipo de lista en el panel principal o usando PCM. El programa acepta que el final de una línea (Enter) es el final del elemento de la lista.
Instrucción paso a paso o un simple algoritmo
Entre la enorme cantidad de listas que se encuentran en un barrio o en otro editor, que no son una lista de nada, sino un plan de acción paso a paso.
Fuente. Fuente. Fuente.
Como se puede ver en los ejemplos, cuando la lista numerada se utiliza simplemente como una descripción de los artículos, los objetos, los artículos pueden ser cambiados en lugares, se obtendrá el objetivo final – el usuario obtendrá la cantidad completa de información.
Para una lista numerada como una instrucción paso a paso, la secuencia de elementos es crítica. Cada paso siguiente sólo puede hacerse después del anterior. Sólo entonces se obtendrá el resultado deseado. Esto se ve claramente en el ejemplo de la receta paso a paso.
Es un algoritmo lineal en el que el proceso se descompone en pasos elementales. Realizando estos sencillos pasos el usuario logrará el objetivo deseado, aunque parezca complejo.
Vamos a crear un simple algoritmo. Como hacer un sándwich de mantequilla y queso.
Para conseguir un sándwich preparado al final, tienes que realizar estos pasos:
- Toma el dinero.
- Ve a la tienda.
- Compra pan, mantequilla, queso.
- Trae la comida a casa.
- Cortar el pan.
- Fríe el pan en una sartén caliente hasta que se triture.
- Aplica una fina capa de aceite a los picatostes.
- Corta el queso.
- Ponga rebanadas de queso en el pan y la mantequilla.
Mira, cada paso del algoritmo es simple y claro. Pero incluso estos simples puntos pueden ser desglosados en pasos aún más detallados. Por ejemplo, tomar el dinero en casa, ponerlo en la billetera, vestirse, zapatos, dejar el apartamento, cerrar la puerta, etc. Los detalles se pueden desglosar en pasos elementales.
El nivel de detalle de cada paso del algoritmo se selecciona dependiendo del nivel del artista. Si el algoritmo se calcula para un principiante, consistirá en los pasos más sencillos, si la persona tiene experiencia, los puntos serán más complejos. Esto es como explicar una nueva receta a un maestro cocinero sin experiencia.
Muchos problemas pueden ser traducidos a una forma universal usando un lenguaje matemático. Y habiendo hecho un algoritmo y habiendo escrito un programa en él, para acelerar, para simplificar el cálculo de la mayoría de las tareas. Sin modelos matemáticos y programación es imposible presentar el cálculo del presupuesto anual, la vigilancia del efecto invernadero, los cálculos en la jardinería y la agricultura.
